PPAD (complexity)

PPAD ("Polynomial Parity Arguments on Directed graphs") is a complexity class introduced by Christos Papadimitriou in 1994. PPAD is a subclass of TFNP based on functions that can be shown to be total by a parity argument.[1][2] The class attracted significant attention in the field of algorithmic game theory because it contains the problem of computing a Nash equilibrium, and this problem was shown by Chen and Deng in 2005 to be complete for the class.[3]

PPAD is a class of problems that are believed to be hard, but obtaining PPAD-completeness is a weaker evidence of intractability than that of obtaining NP-completeness. It could still be the case that PPAD is the same class as P, and still have that P 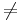\neq NP, though it seems unlikely. Examples of PPAD-complete problems include finding Nash equilibria, Brouwer and Borsuk-Ulam fixpoints, the cutting sandwich problem, finding Arrow Debreu equilibria in markets and more (The Complexity of Finding Nash Equilibria, Papadimitriou).

Contents

Definition

PPAD is a subset of the class TFNP, the class of function problems in FNP that are guaranteed to be total. Its formal definition may be given as follows:

A binary relation P(x,y) is in TFNP if and only if there is a deterministic polynomial time algorithm that can determine whether P(x,y) holds given both x and y, and for every x, there exists a y such that P(x,y) holds.

Subclasses of TFNP are defined based on the type of mathematical proof used to prove that a solution always exists. Informally, PPAD is the subclass of TFNP where the guarantee that there exists a y such that P(x,y) holds is based on a parity argument on a directed graph. The class is formally defined by specifying one of its complete problems, known as End-Of-The-Line:

G is a (possibly exponentially large) directed graph with no isolated vertices, and with every vertex having at most one predecessor and one successor. G is specified by giving a polynomial-time computable function f(v) (polynomial in the size of v) that returns the predecessor and successor (if they exist) of the vertex v. Given a vertex s in G with no predecessor, find a vertex t≠s with no predecessor or no successor. (The input to the problem is the source vertex s and the function f(v)). In other words, we want any source or sink of the directed graph other than s.

Such a t must exist if an s does, because the structure of G means that vertices with only one neighbour come in pairs. In particular, given s, we can find such a t at the other end of the string starting at s. (Note that this may take exponential time if we just evaluate f repeatedly.)

Relationship to other complexity classes

PPAD is contained in (but not known to be equal to) PPA (the corresponding class of parity arguments for undirected graphs) which is contained in TFNP. PPAD is also contained in (but not known to be equal to) PPP, another subclass of TFNP. It contains CLS.

Other notable complete problems

Main article: List of PPAD-complete problems

References

  1. ^ Christos Papadimitriou (1994). "On the complexity of the parity argument and other inefficient proofs of existence". Journal of Computer and System Sciences 48 (3): 498–532. doi:10.1016/S0022-0000(05)80063-7. http://www.cs.berkeley.edu/~christos/papers/On%20the%20Complexity.pdf. 
  2. ^ Fortnow, Lance (2005). "What is PPAD?". http://weblog.fortnow.com/2005/12/what-is-ppad.html. Retrieved 2007-01-29. 
  3. ^ a b *Chen, Xi; Deng, Xiaotie (2006). "Settling the complexity of two-player Nash equilibrium". Proc. 47th Symp. Foundations of Computer Science. pp. 261–271. doi:10.1109/FOCS.2006.69. ECCC TR05-140 .
  4. ^ Xi Chen and Xiaotie Deng (2006). "On the Complexity of 2D Discrete Fixed Point Problem". International Colloquium on Automata, Languages and Programming. pp. 489–500. ECCC TR06-037. 

External links